



Next: Eksamensopgaver i Kemi F
Up: hpage
Previous: O2-O2 rates
Contents
Kemi F
Pensum d. 6 marts: Hückel teori, afsnit 3.6
Opgaver d. 11. marts:
Ex. jan. 1998, opg.3
Ex. juni 1998, opg.2+3
Ex. juni 2000, opg.2
Pensum d. 11+12 marts: Biokemi+Statistisk termodynamik, afsnit 5.1+5.2
Opgaver d. 18 marts:
Ex. 1994, opg. 1+2
Ex. jan. 1999, opg. 3
Ex. juni 1999, opg. 3
Ex. jan. 2000, opg. 2
Pensum d. 18+19 marts: Kemisk ligevægt, afsnit 6.1+6.2+6.3
Undervisning d. 25+26 marts aflyst
2. april: Undervisningsfri
Pensum d. 8+9 april: pH, afsnit 6.4+6.5+6.6+6.7
Opgaver d. 8 april:
Ex. jan. 1995, opg. 2+3
Ex. jan. 1996, opg. 3
Ex. jan. 1996, opg. 5
Ex. juni 1998, opg. 5
Ex. Dec. 95, opg. 4
Pensum d. 15+16 april: Elektrokemi+Kemisk kinetik, afsnit 6.8+6.9+
7.1+7.2+7.3
Opgaver d. 15. april:
Ex. Jan. 96, opg 4
Ex. Jan. 97, opg 4
Ex. Juni 97, opg.4
Ex. Dec. 95, opg. 6
Ex. Jan. 96, opg. 6
Ex. Jan. 99, opg. 6
22. april): Undervisning aflyst.
Pensum d.23 april: Kemisk kinetik, afsnit 7.4+7.5+7.6+7.7
Opgaver d. 29. april:
Ex. Jan. 97, opg 5
Ex. Juni 97, opg 6
Ex. Juni 98, opg 7
Ex. Jan. 99, opg. 5
Ex. Juni 99, opg. 5
Juni 01 opg 1-6.
Opgavegennemgang d. 6. maj er udsat til senere. Der er i stedet
givet en
besvarelse på opgavesættet Jan. 01 (se nf.):
Spørgetime: Mandag d. 10. juni kl. 10 .
Eksamen i Kemi F. 14 juni 2002
|
Eksamensnr. |
Karakter |
|
1 |
10 |
|
2 |
9 |
|
3 |
6 |
|
5 |
6 |
|
6 |
7 |
|
7 |
9 |
|
8 |
6 |
|
9 |
6 |
|
11 |
7 |
|
13 |
5 |
|
14 |
11 |
|
15 |
10 |
|
16 |
6 |
|
17 |
8 |
|
18 |
03 |
|
19 |
6 |
|
20 |
8 |
|
21 |
8 |
|
22 |
6 |
|
23 |
03 |
|
26 |
7 |
|
27 |
8 |
Besvarelse KemiF Jan. 01
Opg. 1
6 6 determinant med
6 determinant med 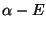 i diagonal og
i diagonal og 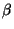 langs
diagonalen samt i element 1,6 og 6,1
langs
diagonalen samt i element 1,6 og 6,1
Laveste energi
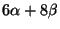 for benzen. For 3 isolerede
dobbeltbindinger
for benzen. For 3 isolerede
dobbeltbindinger
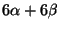 . Delokaliseringsenergi derfor 2
. Delokaliseringsenergi derfor 2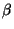 .
.
Opg. 2
Anvend
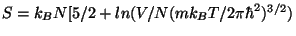 samt
samt 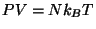 .
.
Opg. 3
a) 2 molekyler CH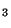 OH; b) CH
OH; b) CH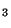 COOH+C
COOH+C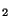 H
H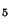 OH; c) C
OH; c) C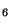 H
H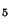 COOH+CH
COOH+CH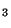 COOH; d) C
COOH; d) C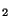 H
H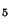 COOH+H
COOH+H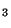 PO
PO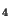 .
.
Opg 4
a) Opløselighed 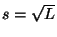 =5.07 10
=5.07 10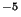 mol/l = 6.49 mg/l.
mol/l = 6.49 mg/l.
b) Her omdannes noget 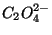 til HC
til HC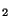 O
O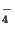 dvs. opløseligheden
stiger. Flg. ligevægte haves:
dvs. opløseligheden
stiger. Flg. ligevægte haves:
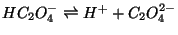
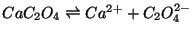
Dvs.
![\begin{displaymath}
\frac{[H^+][C_2O_4^{2-}]}{[HC_2O_4^-]}=10^{-4.19}=K_2=6.46 10^{-5}
\end{displaymath}](img55.gif) |
(1) |
![\begin{displaymath}[Ca^{2+}][C_2O_4^{2-}]=L=2.57 10^{-9}
\end{displaymath}](img56.gif) |
(2) |
Opløselighed er givet ved
![$[Ca^{2+}]=[HC_2O_4^-]+[C_2O_4^{2-}]$](img57.gif) (3)
Endvidere haves
(3)
Endvidere haves
![$[H^+]+[HC_2O_4^-]=0.01 M$](img58.gif) (4).
(4).
Udfra de tre første ligninger fås:
![$[C_2O_4^{2-}]=\sqrt{\frac{L}{1+K_2/[H^+]}}$](img59.gif) Antag først
Antag først ![$[H^+]=0.01$](img60.gif) (1. iteration). Dette giver
(1. iteration). Dette giver
![$[C_2O_4^{2-}]=4.06 10^{-6} M$](img61.gif) og
og
![$[HC_2O_4^-]=6.29 10^{-4} M$](img62.gif) .
.
Udfra (4) fås ![$[H^+]=0.0093$](img63.gif) . Med denne værdi fås (2. iteration)
. Med denne værdi fås (2. iteration)
![$[C_2O_4^{2+}]=4.21 10^{-6}$](img64.gif) samt
samt
![$[HC_2O_4^-]=6.06 10^{-4}$](img65.gif) etc.
etc.
Opløselighed defineres ved
![$[Ca^{2+}]=6.11 10^{-4} M$](img66.gif) eller 78.3 mg/l.
eller 78.3 mg/l.
Opg. 5
a) 1/2(9.25+2)=5.6 (svag syre); b) pOH=1/2(2+7.63)=4.8 pH=9.2 (svag base);
c) 1/2(7.21+12.3)=9.6 (amfolyt); d) pOH=1/2(2+7.63)=4.8 pH=9.2 (svag base).
Opg. 6
1)
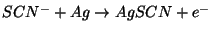
2)
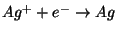
Celleprocess:
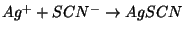
For denne process er
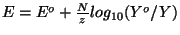 =0.586 V. Vi har
desuden
=0.586 V. Vi har
desuden
![$Y=\frac{x_{AgSCN}}{[Ag^+][SCN^-]}$](img71.gif) =1/(0.1
=1/(0.1 0.1)=100.
Dvs.
0.1)=100.
Dvs.
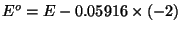 =0.586+0.118=0.704 V.
=0.586+0.118=0.704 V.
b) Dvs. 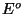 for den modsatte process er -0.704 V og ligevægtskonstanten
for den modsatte process er -0.704 V og ligevægtskonstanten
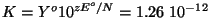 .
.




Next: Eksamensopgaver i Kemi F
Up: hpage
Previous: O2-O2 rates
Contents
Gert D. Billing
2002-07-01